G-3: The Input Bar

One of the most powerful features in GeoGebra is the Input Bar. This lesson will introduces Input commands, some of which mimic the tools you are already familiar with, and some of which are completely unique to the Input Bar.

Anything You Can Do, I Can Do Better (or just differently)

We mentioned in G-1 that under object properties, the ‘Definition’ attribute described the code that could be used to generate the object from the Input Bar. Try drawing some of the objects you use more frequently, and take a look at the command that is used to generate them. In particular, look at the following tools and methods:

• New Point (Free and Path Dependent Point)
• Intersect Two Objects (Try using the New Point method on the two intersections of a circle and a line vs using this tool)
• Line through Two Points
• Perpendicular Line
• Parallel Line
• Circle with Center through Point
• Circle with Center and Radius
• Circle through Three Points

Pick a couple of these and then try entering that same type of command manually on the Input Bar.

New Points and Vectors

Unlike all the other objects created above, the object properties of Free points are unique. Rather than having a definition, they simply have a value property. Therefore, to create a New (Free) Point, type the coordinates of a Point into the Input Bar and click enter. Try entering (1,2).

To specify a name when you create the point, write the name, followed by : or = followed by the coordinates of your point. Try entering P:(3,1), then try q:(2,2).

Wait! The second attempt did not give a point, but a vector! When a lowercase letter is assigned Cartesian Coordinates, GeoGebra assumes you are trying to create a vector. Vectors are not covered in this week’s material, but feel free to experiment with them if you wish. If you want to create a point with a lowercase name, create the point first, then rename it after its creation.

Commands with Multiple Syntaxes

You will note that several of the tools listed above use the same command. GeoGebra determines the object you wish to create by looking at the types of objects provided to the command. For a list of accepted syntaxes, simply type the name of the command in the Input Bar, and a list of possible syntaxes will appear. In addition, other commands starting with the same letters as the written command will appear. Additionally, if you enter a command incorrectly, a window will appear with the accepted syntaxes.

Nameless Arguments

Recall that for tools which require points, one could click anywhere in the graphics view to create the needed point. In the input bar, a similar thing can be done when a command needs an argument.

For example, I could create a line through (1,0) and (0,1) by typing Line[(1, 0), (0, 1)]. Unlike the tool, the additional points used do not appear in the Graphics View. Indeed, they are not even defined objects.

This can actually be done for any type of object, not just points. Try typing PerpendicularLine[(0, 4), Line[(1, 0), (0, 1)]].

Sliders are Variables

Locate and select the Slider tool. Click somewhere in the Graphics View and the following window will open.

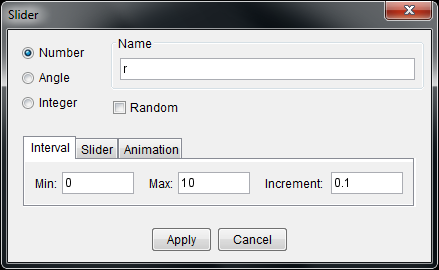
Change the Name field to ‘r’, the Min field to 0 and the Max field to 10. Click Apply. You have created a variable! This variable can now be used anywhere a number would normally be needed. Use the Circle with Center and Radius tool to create a circle centered at the origin with radius ‘r’.

Experiment with the Move tool and the  Move Graphics View tool to see what happens to the newly created slider. You will be able to adjust the value of the slider, and therefore the radius of the circle, but the slider cannot be moved from its position on the screen. If you look through the Object Properties of the slider, you will note that there are two properties explaining the positioning of the slider. Under the Basic tab the option “Absolute Position on Screen” is checked, and under the Slider tab, the option “Fixed” is checked. These are set by default, but feel free to adjust them as you see fit.

Create another slider, but this time, choose the Angle option instead of Number (leave the Name, Min and Max fields at their default value). This slider seems very similar to the last one, but note that an angle is seen as a different kind of object than a number (see the Object Properties). In addition, angles are given greek letters as names by default. Create a point ‘P’ at the intersection of the circle and the positive x-axis. (What method do you use when you only want one intersection?) Then use the  Rotate Object around Point by Angle tool to rotate ‘P’ around the origin counterclockwise by α. In order to insert a symbol, click the alpha button at the right side of the input bar. We have now created a point with polar coordinates (r, α)!

Finally, if you prefer to use the Input Bar, you can always create a variable by simply typing a number into the Input Bar (to assign a label at the same time, follow the instructions from before). The variable appears in the Algebra View. If you wish to create a slider for this variable, simply show the object. If you wish to leave it hidden but would like to change the value, double click on the variable in the Algebra View.

Equations and Functions

When creating lines and circles, you may have noted in the Algebra View that these objects were assigned equations in x and y representing their paths. It turns out that the Input Bar is capable of handling any equation in x and y, given that the degree of any term is an integer between 0 and 2 inclusive. Try typing the equation x^2 - x*y + y^2 = 1 in the Input Bar. This path can then be interacted with like any other normal object.

In addition to equations in x and y, we can also create functions in x using the Input Bar. Functions are not restricted to terms with integral degree. Try typing f(x) = sin(x) in the Input Bar. Again, this path can now be interacted with like any other object. However, we also have the option of using \(f(x)\) to obtain a numerical value (e.g. create the point (3, f(3)).)

For a list of all mathematical functions (such as sin) as well as GeoGebra commands (such as Line), click on the button at the far right of the Input Bar.