M-7: Random Walks Case Study

In this lesson we run through the process of programming Maple to:

• simulate a random 2D walk
• calculate the squared distance of a walker from the origin after N steps
• give the sample mean and sample standard deviation from T trials of this process

We’ll be using structured programming and procedures to complete the task, which breaks it up in to some small parts. In general, working on any significant programming task is easiest if you work in small batches: make a small amount of code, run it to see that it doesn’t crash and test it to make sure it behaves as expected, and then make one more small addition after that. This prevents the issue of “I have no idea why my 100 lines of code are not working.” For some more general practice and information on debugging you might find this CS Circles lesson useful.

The description below skips all of the false starts and trial-and-error that would really be involved in creating a significant amount of Maple code. Even so, you can see right at the end that it needs some significant change to be made more robust.

The Plan

The specific random walk that we have in mind is: the walker will always be at a pair of integer coordinates, starting at (0, 0); and at each step, randomly chooses one of its 4 immediate neighbours (up, down, left, or right).

One of the interesting things about such a random walk is that the behaviour is quite different if we go up to 3D. There is a well-known quote by the mathematician Shizuo Kakutani saying

A drunk man will find his way home, but a drunk bird may get lost forever.

What this specifically refers to is that in 2D the probability of ever having returned to the origin approaches 1 as time increases, but in 3D the probability is almost 66% that the random walker never returns to the origin.

Anyway, having that in mind, our goals give us a few natural objectives in terms of what procedures we’d like to create:

1. A procedure (let’s say randomWalk) that, on input N, outputs the final position after a random walker starting at the origin takes N steps.
2. A procedure (let’s say walkerDistances) that, on input N and T (the number of trials) outputs a list of length T representing the squared final distances from the origin from T trials of length N each
3. Code to take enough samples, plot the frequencies, and compute the mean and standard deviations.

We’ll keep our code flexible, easy to understand, and able to use any number of dimensions, by using a variable d instead the constant 2.

> d := 2;

Next, by looking up ?rand we find that there is a way to create random numbers from any specified range: rand(a..b) will return a procedure that generates random integers from a to b. (For this reason we would call rand a “higher-order procedure”: it is a procedure that returns a procedure.) We’ll need this for the random walk in two ways:

> randomDimension := rand(1..d):
> random01 := rand(0..1):

With this, we’re ready to create the procedure randomWalk(N) described above. It takes a d-dimensional random walk for N steps and then returns the final position as a list. Note that we use the [seq(0, i=1..d)] idiom for creating a list of length d.

> randomWalk := proc(N)
     local pos, i, axis, step:
     pos := [seq(0, i=1..d)]:
     for i from 1 to N do
        axis := randomDimension();
        step := -1 + 2*random01(); # gives -1 or +1
        pos[axis] := pos[axis] + step;
     end:
     return pos:
  end:

Note: I (the author) invariably write the procedure first and then wait for Maple to warn me about what variables should be declared as local. It is not necessary to get everything perfect in the first step.

At this point, let’s see if our random walk works:

seq(randomWalk(11), i=1..20);

It looks pretty reasonable: it gives back the list [0, -1], [0, 1], [-1, 0], [-3, 2], [3, 0], [6, 1], [-2, 3], [1, -2], [1, 0], [4, 3], [-4, 1], [3, 6], [-1, -2], [-2, -1], [0, 1], [1, 2], [-1, 2], [3, -4], [5, 0], [0, -1] of 20 random walk endpoints, with 11 steps per walk.

Moving on, let’s define the walkerDistances(N, T) procedure described earlier, which gives the final squared distances for T trials, each one of N steps. Aside from the for loop, we’ll have to call randomWalk, and compute the squared distance using the Pythagorean theorem.

walkerDistances := proc(N, T)
  local result, i, pos, squaredDistance:
  result := [seq(0, i=1..T)]:
  for i from 1 to T do
     pos := randomWalk(N): # pos: final position
     squaredDistance := sum(pos[j]*pos[j], j=1..d):
     result[i] := squaredDistance;
  end:
  return result;
end:

Again, it’s best to test this right away.

> walkerDistances(15, 30);

It looks pretty reasonable: the output is [1, 1, 13, 5, 5, 45, 1, 5, 17, 1, 5, 29, 25, 41, 1, 9, 25, 1, 65, 53, 5, 1, 29, 9, 1, 17, 1, 5, 65, 25] which seems it could be the final squared distances after 11 steps, over 30 trials.

Finally, we have the problem of plotting the data. We’ll use the plot procedure on a list of points, putting the squared distance on the x-axis and the frequency on the y-axis; recall that this means we need to get the points in the format [[x1, y1], [x2, y2], ...]. It makes sense to encapsulate this complicated step into a procedure frequencies, since it’s just taking one kind of data and transforming it into another format. Two things are notable about this code: it has to be careful to allow for the possibility that the value 0 occurs, which requires shifting list indices by 1; and it uses nops() to get the length of the input list data.

> frequencies := proc(data)
    # input: a list of values
    # output: a list of 2-element lists of the form [value, frequency]  
    local maximum, n, i, frequency, result:
    # find the maximum of all the data values, needed for tabulation
    maximum := data[1];
    n := nops(data);
    for i from 2 to n do
       maximum := max(maximum, data[i]):
    end: 
    # tabulate into the list "frequency" 
    # frequency[j+1] will represent the frequency of j 
    frequency := [seq(0, i=1..maximum+1)];
    for i from 1 to n do
       frequency[data[i]+1] := frequency[data[i]+1] + 1;
    end:
    # finally get it into the exact right format  
    result := [seq(0, i=1..maximum+1)];
    for i from 0 to maximum do 
       result[i+1] := [i, frequency[i+1]];
    end:
    return result;
  end:

Again, it’s good to test this on a small input:

> frequencies([9, 6, 7, 1, 1, 1, 1]);

yields [[0, 0], [1, 4], [2, 0], [3, 0], [4, 0], [5, 0], [6, 1], [7, 1], [8, 0], [9, 1]], which looks good. Finally, we put everything together: let’s look at 100 trials, where the walkers take 16 steps each.

> trials := 100; steps := 16;
> distances := walkerDistances(steps, trials):
> plot(frequencies(distances), style=point);
> mean := evalf(sum(distances[i], i=1..trials)/trials);
> squareSum := sum(distances[i]*distances[i], i=1..trials);
> stddev := evalf(sqrt(squareSum/(trials-1)));

Here’s what it looks like:

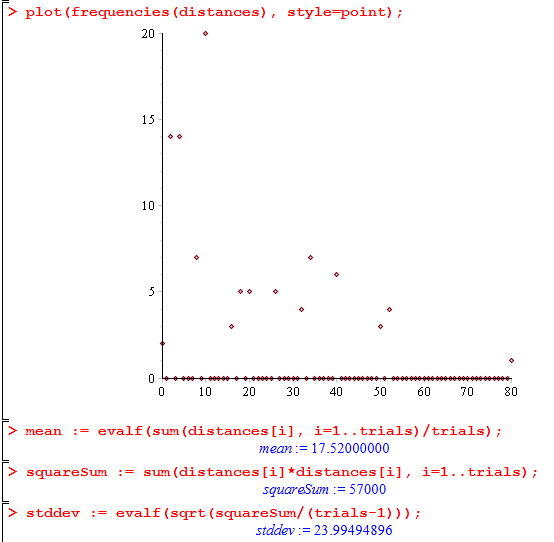
You can download the entire worksheet here.

Caveat listor; using Arrays and tables

In fact, this experiment pushes the limits of what lists can do. If you try to take one even more trial, you get the error “assigning to a long list, please use Arrays.” This is because manipulating a list takes time proportional to its length. Maple has other data structures that are more suitable when you want to modify a large set of data. We’ll just introduce the two most fundamental ones here, Arrays and tables. Their similarities are:

• both are discrete maps from inputs to outputs
• both can contain an unlimited amount of data
• neither has to be initialized with an explicit size in mind: there is always room for one more input/output pair
• both can be accessed and updated in a small time that does not depend on their size

Their differences are:

• tables can take any possible inputs
• Arrays can only take inputs that are integers or k-dimensional sequences of integers
• Arrays are stored as complete k-dimensional grids (unless initialized with storage=sparse)

Since tables are simpler and likely to suffice for most purposes, we’ll introduce them first. (If you’re doing linear algebra, however, check out the Matrix relative of Arrays.) You create an empty table with table() (analogous to {} for sets). Then, you access or insert elements by using the [] operators. For example,

> t := table();
> t[1] := "one":
> t[3] := "three":
> t[{}] := "the empty set":
> t[x^2] := "ex squared":
> t[5, 4] := "five comma four":

will create a new table with 5 input/output pairs. If you just evaluate t; it yields the value table([1 = “one”, 3 = “three”, x^2 = “ex squared”, {} = “the empty set”, (5, 4) = “five comma four”]). Subsequently when you write t[1] it evaluates to “one” (unless you overwrite it later of course, for example with t[1] := "unity").

You can convert a table to other formats, such as myList := convert(t, list) or mySet := convert(t, set). As usual, see ?table for the definitive details.

Here is an example of what we mean by Arrays being stored as a consecutive grid. Note that we use round parentheses () instead of square brackets [] to contain the index in this example:

> A := Array():
> A(2) := "two":
> A(5) := "five":

Then, evaluating A; will give back [ 0 “two” 0 0 “five” ]. Furthermore, if we go on to set A(2, 3) := "new"; we’ll see that A; changes to look like the following:

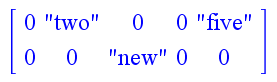
It takes some care to work with Arrays, but they are quite flexible: you can initialize an Array with predefined ranges like Array(-2..2, 10..20); and you can access Arrays using [square brackets] which always index starting from 1. See the Maple reference webpage on data structures, or ?Array, for more information.