M-5: Structured Programming
In this lesson and the next one we introduce the basic concepts of structured programming: loops, conditionals, and (in the next lesson) procedures. We will not go as slow as basic introductory material (see CS Circles for such a level of explanation but in Python), but we’ll give examples as we go along.
Our lessons try to give a short but comprehensive summary of the most important tools that a Maple programmer needs to know how to use. But you can always find out more information from the Maple programming guide which gives a more narrative description than the ? help pages.
We’ve already seen the seq() command, which lets you define a sequence of items by iterating a base expression many times. For example, seq(x^2, x=1..5) gives the sequence 1, 4, 9, 16, 25. However, sometimes what you want to repeat is more complicated than a simple expression like x^2. An excellent example is, evaluate the first 10 partial sums of the power series
\(\exp(x) = 1 + x + x^2/2! + x^3/3! + \cdots\)
at \(x=0.6\). In principle we can do this using nested seqs but let’s try doing it in a more natural way.
What we want to do can be explained in plain English:
- Keep a running sum, initialized to zero.
- Repeat the following steps, starting at k=0 and repeating with k=1, 2, … until k=9:
- Add \(0.6^k/k!\) to the running sum
- The value of the running sum is the kth term in the series
This is how we’d write it in Maple.
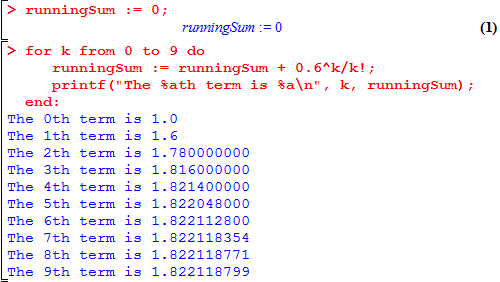
> runningSum := 0;
> for k from 0 to 9 do
runningSum := runningSum + 0.6^k/k!;
"The ", k, "th term is ", runningSum;
end;
At this point, we want you to try writing it yourself. To do this, press Shift-Enter instead of just Enter to finish the second, third, and fourth lines. That is to say,
> runningSum := 0; # press ENTER
> for k from 0 to 9 do # press SHIFT-ENTER
runningSum := runningSum + 0.6^k/k!; # press SHIFT-ENTER
"The ", k, "th term is ", runningSum; # press SHIFT-ENTER
end; # press ENTER
If you got this to work, you’ll see a bunch of blue output (see below). But to hit possible problems off at the head, we will discuss the formatting in more detail. The reason for that you needed to press SHIFT-ENTER is that the whole for loop (from for… to … end) should lie within a single Maple “execution group.” Execution groups are the [-shaped things on the left-hand side of the screen.
Because this is a little tricky, we show here an example of correctly inputting the for loop versus doing it incorrectly. Here’s what a correct version looks like:

Here is another version that runs. It works, but it is functionally a little different because you are forced to always initialize the running sum and evaluate the for loop since they’re in the same execution group. As well, there are multiple command prompts (>) in a single execution group, which has no substantive effect but makes it harder to read.
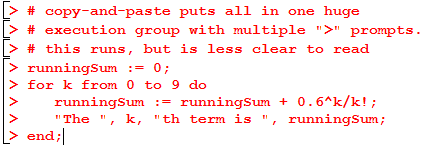
Finally, here’s a version that will not run.

If you end up with such a version, try selecting all the lines and using Edit > Split or Join > Join Execution Groups (or F4).
Back to the actual code. If you followed the original instructions, your output will look like this:

Awesome! More than just this basic example, let us now give the general syntax and structure of a for loop. Caveat: the spaces at the front of each line are not required (specifically, e.g., the three spaces before runningSum := runningSum + 1), they are totally ignored by Maple. However, it’s always a good idea to use this kind of indentation to make your code clearer for yourself and others who might read it. Likewise, in our examples, the interior of a nested loop will be indented by 3+3=6 spaces, a triply-nested loop by 9 spaces, etc.
A general version of the for loop is:
for «loopVariable» from «minValue» to «maxValue» do «body» # possibly consisting of several lines end;
This tells Maple precisely to set the loop variable to «minValue» and then to execute the body, then to set the loop variable to «minValue»+1 and to execute all steps in the body again, etc, with the last loop being the one where the loop variable has value «maxValue». Take a minute to see how this generic syntax compares with the example above, and how the outputs correspond to the exact lines that Maple executes (and the order in which they are executed).
It is very important to follow the syntax including do and end or else Maple won’t be able to understand you. Sometimes, you might want the loop variable to be decreasing, or to go up in steps of size greater than 1: to do this, look up the syntax in ?for.
An instructive question: how many times will the body be executed in such a for loop? Answer: (maxValue – minValue + 1). Forgetting the +1 can be a common source or errors.
When it comes to loops, Maple’s rules for ; versus : are a bit different: if the loop is terminated with end: then no output will be printed, and if it is terminated with end; then all outputs will be printed. It does not matter whether the lines in the body of the loop end with ; or :.
Printing Nicely
The paragraph above makes it unclear how we can execute the output of our for loop in a nicer format: we want to hide the first line in the body, and show the second. Additionally, the second line’s output is pretty ugly. To get around this, we are going to use the formatted print command printf().
The way that we will use printf is by replacing the line
"The ", k, "th term is ", runningSum;
with
printf("The %ath term is %a\n", k, runningSum);
The first argument to printf is a template (or format string). In this example, the template says that we want a string that looks like The Xth term is X but we want the first X replaced with the value of k, and we want the second X replaced with the value of runningSum. The %a is a generic format specifier; if you are interested in the different ways that you can format output, check out ?printf. The \n is needed to end a line (see what happens if you leave it out).
Finally, if
- we modify the line above to use
printfas indicated - we change the
end;terminating the loop toend:
we’ll get a program that shows us this output:
There are other variations possible depending on your goal. We could replace the printf line with just
print("The", k, "th term is", runningSum);
and you’ll see that it gives the right information, but is harder to read. Another advantage of learning printf is that it’s just one letter away from fprintf, which lets you write output to text files.
While Loops
The for loop is great when you have a predefined start and end value for your variable. However, it’s sometimes the case that you don’t know your destination until you get there.
As a concrete example, let’s say that we want to follow the example above, but instead of specifying the number of terms in advance we just want however many terms are necessary until we have a value that is accurate to \(\pm10^{-20}\). Consider the following code:
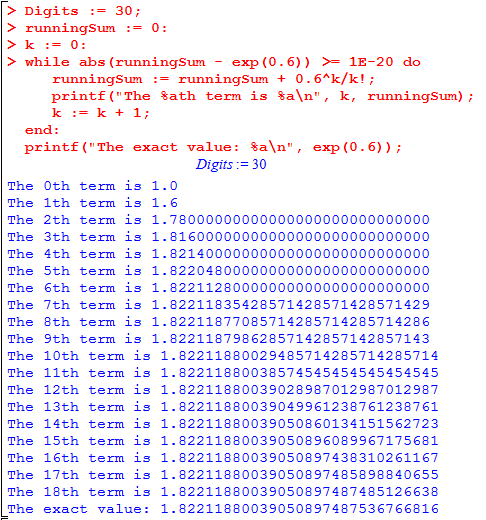
> Digits := 30;
runningSum := 0:
k := 0:
while abs(runningSum - exp(0.6)) >= 1E-20 do
runningSum := runningSum + 0.6^k/k!;
printf("The %ath term is %a\n", k, runningSum);
k := k + 1;
end:
printf("The exact value: %a\n", exp(0.6));
We use a few simple new features:
Digits, the global variable controlling floating-point accuracy1E-20, scientific notation for \(1 \times 10^{-20}\)abs, the absolute value function
That having been said, how does a while loop operate? Its general form is
while «test» do «body» # possibly multiple lines end
Here, test should be some boolean (true/false) expression. When Maple comes to execute the loop, it checks the test. If the test is true, then the body is executed. But once the end is reached, it runs again: the test is checked again, and the body is executed again. Only once the value of «test» is false does the loop end. Afterwards, Maple keeps computing the following lines. In the example above, this yields
Again, compare the generic form with the specific example and see that Maple does the same thing you would do if you evaluated these commands by hand.
Infinite Loops
An inevitable consequence of working with while loops is that you will sometimes make your computer enter an infinite loop. For example, if you forgot to write k := k + 1; in the above example, then since a while loop (unlike a for loop) doesn’t automatically increment any counters, it would run forever. Try it! — but be prepared to stop it. The way to stop an infinite loop in Maple is by pressing the red stop sign button with a hand on it: ![]() , at least in the latest version (at least on Windows). As far as we know, there’s no keyboard shortcut for this.
, at least in the latest version (at least on Windows). As far as we know, there’s no keyboard shortcut for this.
Conditionals: The if statement
Sometimes you want to execute a collection of lines or not, depending on some particular conditions. Keeping with the theme of our examples above, let’s move from the exponential power series to the power series of the sine function,
What would it take to modify the most recent example (approximating within \(10^{-20}\)) to work with the sine function? The main difficulty is that we only want the term to be added to the power series when k is odd. For this, we use the following code:
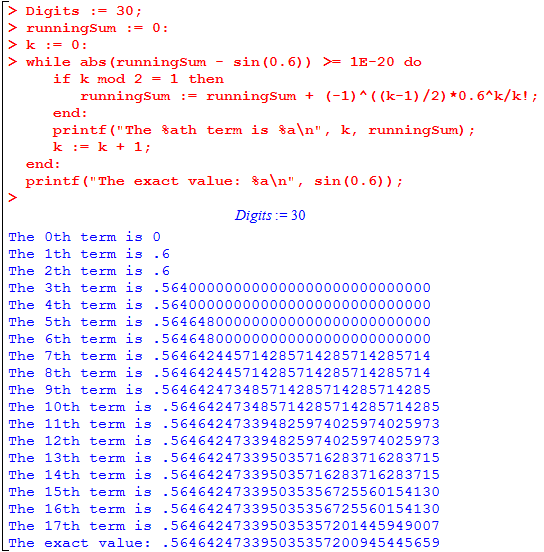
> Digits := 30;
runningSum := 0:
k := 0:
while abs(runningSum - sin(0.6)) >= 1E-20 do
if k mod 2 = 1 then
runningSum := runningSum + (-1)^((k-1)/2)*0.6^k/k!;
end:
printf("The %ath term is %a\n", k, runningSum);
k := k + 1;
end:
printf("The exact value: %a\n", sin(0.6));
Note that we are nesting an if statement inside of a while loop: there is no limit to the nesting that is allowed. Also, note that this is our first use of the mod operator.
The general format of an if statement is:
if «test» then «body» # possibly multiple lines end
It’s worth yet again comparing the generic example with the specific one given above. Note in particular that because of how we structured our code, the printf statement and increment-k statement are executed regardless of whether k mod 2 = 1 was true. The output is shown below:
else and elif
Finally, we would like to put one last finishing touch on the program. We should replace 1th with 1st, etc, making it use proper English. This is an excellent opportunity to use an else statement. As the name suggests,
if «test» then «body» # possibly multiple lines else «alternate body» # possibly multiple lines end
means that we execute the body when the test is true, and the alternate body when the test is false. An extremely common situation is that we want to chain together several if-else statements. For this, we can use elif as a replacement for else if; it changes nothing substantive but makes your code a lot easier to read and debug. In our example we’d write
if k = 1 then suffix := "st"; elif k = 2 then suffix := "nd"; elif k = 3 then suffix := "rd"; else suffix := "th"; end:
Suggested challenges:
- Incorporate this block of code with the previous examples. Use
%sin place of%ainprintfwhen referencing thesuffixvariable to avoid getting unwanted quotes. - The above block of code is not accurate for all values of
k, e.g.k=21. Try to fix it so that works for all possible integer values ofk. The simplest version of the code will usemodas well as theorandandboolean operators (see?andfor details).
The `if` function
Sometimes, you might want to write down a conditional statement without writing multiple lines of code, for example in the body of seq. For this you can use the `if` function, which always takes exactly three arguments,
> `if`(«test», «Tvalue», «Fvalue»);
It checks the value of the test and returns the Tvalue if the test is true, and the Fvalue if the test is false. For example, we can define the absolute value function by
> absValue := x -> `if`(x>0, x, -x);
(As we mentioned earlier, this function is already pre-defined in Maple as abs.)
Postscript (not the .ps file format)
In our examples, we checked for “approximate convergence” of the power series by comparing it to the exact value of exp(0.6) or sin(0.6). A computer which is trying to compute sin(0.6) essentially computes the value using power series. But obviously, if it’s trying to compute exp(0.6), it won’t have access to that value already. This is one reason for wanting to prove rigorous convergence bounds that give an unconditional guarantee on the error term.