3-0: Your Wish Is Your Command

Welcome to the final week of LaTeX!  Please note that there are no exercises integrated with the lessons this week, as Assignment 3 is its own project.  We recommend that you read the specifications of the assignment before continuing with the readings in order that you will be able to better plan for the assignment. As well, you may want to try the techniques for practice on your own, as we go through them.

One general technique we introduce this week is defining your own commands. This is done using \newcommand. The simplest usage is to create a short-hand for something that you want to avoid writing over and over: in this case you can create a new command that takes no arguments (inputs). For example, let’s say that you are going to be writing \mathbb{Z} a lot in your document, to denote the set of integers. After writing this a hundred times, you might wonder why there isn’t a shorter way to write this.

Here is how you can create a new command \Z which will print out \mathbb{Z}:

\newcommand{\Z}{\mathbb{Z}}

You can try adding this to the preamble; then see what $|\Z \times \Z| = |\Z|$ looks like.

In general, \newcommand takes two arguments: the new command name which must begin with \, and then the commands you want to be inserted each time it is called. It’s not required, but we recommend that you put all such definitions in the preamble, just to make it easier to see all the definitions at once.

• Occasionally you’ll do this but get an error because such a command name already exists. Use \renewcommand instead to get around this (with caution). For example, by default \P means the pilcrow sign ¶, but if you want it to instead denote the power set operator, use \renewcommand{\P}{\mathcal{P}}.

A side bonus of using \newcommand is that, if you later decide you want the integers to be represented by \mathbf{Z} (\(\mathbf{Z}\)) instead of \mathbb{Z} (\(\mathbb{Z}\)), you can change all occurrences in the whole document just by editing the single command definition to \newcommand{\Z}{\mathbf{Z}} without touching a single \Z.

Getting In An Argument

LaTeX is a full-fledged programming language. A baby step towards this is that things defined by \newcommand can take in one or more inputs (a.k.a. parameters or argument) which the command definition can utilize, adapting the inserted commands each time it is used.

Here is one simple example; the general syntax will be given after. Suppose we put this in the preamble:

\newcommand{\expectation}[1]{ \mathsf{E}\left[ #1 \right] }

This is saying, “Define a command called \expectation which takes one input. When called, print out a copy of that input, surrounded by brackets and the letter E.” We can then call it repeatedly like so:

For any random variables $X$ and $Y$, we have $\expectation{X+Y}=\expectation{X}+\expectation{Y}$
by linearity of expectation.

Each call of the command produces the E and brackets:

General form of a new command

The syntax in general is \newcommand{name}[number of args]{body} and inside of the body, we refer to the arguments by #1, #2, etc. Here are a few more examples, including a function definition where we use an argument more than once (zetafunc), and a function definition that takes in two arguments (hypot).

% in preamble
\newcommand{\expectation}[1]{ \mathsf{E}\left[ #1 \right] }
\newcommand{\zetafunc}[1]{ \zeta(#1) = 1^{-#1} + 2^{-#1} + 3^{-#1} + \cdots }
\newcommand{\hypot}[2]{ \sqrt{#1^2 + #2^2} }
% in main document
$\expectation{\binom{x}{3}}$
$\zetafunc{2012}$
$\hypot{a}{b}, \hypot{\hypot{3}{4}}{12}$

yields

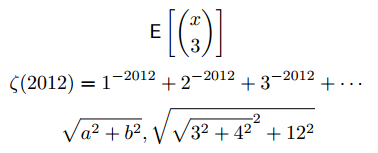
For example, we called \zetafunc on the argument 2012, and this just gives back the body of zetafunc’s definition with #1 replaced throughout by 2012.

A useful trick that can be achieved in this way is to allow for multi-line comments. Define

\newcommand{\comment}[1]{}

The command \comment defined in this way takes one argument (arguments can span any number of lines) and then prints nothing. For example,

3 + 4 =\comment{
old version: \textbf{34}

... my coauthors made me double-check on my fingers.}
7

yields just the output 3 + 4 = 7.

Notes:

• avoid using \def, which is an older way to create new commands
• there are lots of more advanced scripting and programming techniques that we are not discussing here, including optional arguments, defining new environments, and creating packages.