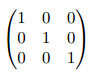2-3: Tables and Arrays

In this lesson we explain how to create LaTeX data that is aligned in rows and columns:

• the tabular environment, which creates tables in text mode;
• the array environment, which creates tables in math mode;
• and the matrix family of environments, which creates tables [in various kinds of brackets] in math mode.

You don’t need any special package to use tabular or array, but you’ll need to use the amsmath package to get the matrix-type commands.

Tip: LaTeX also has a table environment but it not what we’re talking about here. A table is the same as a figure except in name; they are “floating” content containers. We’ll discuss them both later on.

Tip: this is not the preferred way to typeset binomial coefficients (see binom in Section 2-1), “if/else” formulas (next week cases deals with this), or multi-line equations (also next week).

Go (Type)Set The Table

We will start by describing how to use the tabular environment. To use it in the most basic form, you need to know the following:

• when beginning the environment you must pass it a list in curly braces, describing the format of all of the columns;
• you use the alignment character & to indicate the end of a column and the beginning of a new column;
• and you use the newline character \\ to indicate the end of a line and the beginning of a new line.

It is illustrative at this point just to give an example. Here is a chunk of latex code, and the tabular display that it produces:

\begin{tabular}{rl}
Northwest Territories & Nunavut \\
Manitoba & Saskatchewan \\
\end{tabular}

In this example, the list of columns is {rl}, which indicates a right-justified column followed by a left-justified column. The & and \\ delimit the contents of the cells; the last \\ is optional.

To drive home a familiar point, LaTeX will totally ignore the input whitespace; only & and \\ can tell it how everything should be displayed. (It is a common error to forget to put \\ at the end of a line, if you might think that starting a new line would give you a new line in the output.) You can smash the entire grid on one line: \begin{tabular}{rl}NWT&NU\\MB&SK\end{tabular} would give you basically the same result as before.

Lines and Columns

In the column specification, we already saw r and l; other options include

• c for a centred column
• | for a vertical line (you can also put 2 or more in a row)
• p{1cm} for a column of fixed width 1cm; cells with too much text will contain multiple rows.
  • 1cm can be replaced by any other length that LaTeX understands including mm, in, and programmatic lengths
  • you can use \newline within such a cell to force a line break

We won’t use p{} much in our lessons. If you want even more control and options for tables, you should read the documentation for the array package.

For a horizontal line, you can use the command \hline. It should only be used after \\, or at the very beginning.

Here’s the same example as before, but with several horizontal and vertical lines added:

\begin{tabular}{||r|l||}
\hline \hline
Northwest Territories & Nunavut \\
\hline
Manitoba & Saskatchewan \\
\hline \hline
\end{tabular}

You may be able to tell what it will do by looking at the code; run it if you want to see the commands in action.

Occasionally, you will want more space or less space in between the rows of a table. You can use the command [1cm] immediately after \\ to create 1cm of blank space. (For space after a hline, don’t do this, which will crash: \\ \hline [1cm]. Instead add another \\ after the \hline.) Though the [1cm] command works in regular text as well, we do not recommend it; we’ll cover the general vertical spacing commands like \vspace later.

You can created cells with a “merged cell” effect in LaTeX by using the \multicolumn command or the multirow package. We won’t cover this in detail but you can see more information here.

You can put math inside of a tabular environment using $inline math$. But if all of the cells will be mathematical, you can save yourself the trouble of wrapping every single cell in dollar signs by using…

Tables in Math Mode: array

The array environment has the same syntax and usage as tabular, but it must appear inside of a “math mode” (e.g. between $ or $$). Likewise, all of the cells inside of an array environment will automatically put their contents into math mode. In all other aspects, the same instructions above for tabular apply just as well to array.

Even if you wrap the outside of the array in $$display math$$, the cells will be treated as $inline math$. While you can use \displaystyle to get around this, it’s often more visually pleasing in the row-column format to just avoid complicated expressions and instead ensure everything reads simply from left to right. Here is an example, where \frac would not look very nice and instead / was used.

Don’t forget about the \left and \right commands.  They can be used to turn an array into a matrix.  Alternatively, you could just use the matrix.

What is the matrix?

If you include the amsmath package, you will be able to access several additional commands. As the name implies, they are particularly well-suited to typesetting matrices, but they have other uses too.

Like array, we use matrix in math mode. The differences are:

• matrix uses a little less space.
• matrix doesn’t take a list of columns as a parameter. Instead, everything is centred.
• matrix has variants that come with brackets and other delimiters automatically.

What variants, you ask? The simplest one is pmatrix, which typesets its contents in parentheses:

$\begin{pmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{pmatrix}$

gives

The other environments in this family are bmatrix (square brackets []), Bmatrix (curly braces {}), vmatrix (vertical lines | |), and Vmatrix (double vertical lines || ||).

Small Matrices

You also can produce matrices that are small enough to fit in-line with text, by using the smallmatrix environment. They don’t come with the brackets included; you should specify them yourself. For example,

The determinant of $(\begin{smallmatrix}
a & b \\
c & d \\
\end{smallmatrix})$ is $ad-bc$.

will give