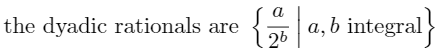2-1: Mathematical Symbols

In this lesson we’ll discuss:

• symbols,
• different shapes and sizes of parentheses,
• and a little bit about tweaking horizontal spaces (kerning) in math mode.

Additional Symbols in Math Mode

So far, the mathematical expressions and equations we have designed have used letters, numbers, and symbols all found on the keyboard (except for a few special functions we introduced).  However, there are a vast number of symbols available in LaTeX in addition to keyboard characters that can be used by calling a particular function. 

\times  \div  \equiv  \neq  \ne  \geq  \ge  \leq  \le  \not\le  \forall  \mid  \exists  \in  \not\in  \notin  \ni  \pi  \theta  \alpha  \beta  \rightarrow  \Rightarrow

For most of these commands, if you attempt you use them outside of math mode, you will receive an error.

Here are a few comments about the symbols above:

• Occasionally you will find two different commands that appear to give the same output.  Sometimes they are in fact identical, other times they may have different rules regarding spacing, or sometimes their differences lie in how they handle superscripts and subscripts.
• Capitals are seen as different characters than lowercase letters; for example, including a capital in \Rightarrow changed the symbol.
• In addition to the greek letters above, all lowercase greek letters are supported (with the exception of omicron).

Exercise (nickname: lines)

What is the difference between \mid, |, \setminus, and \backslash? Using some of these symbols, typeset the following:

As a reminder, we used \textbackslash previously; that works only in text mode, while \backslash works only in math mode.

You have also seen the symbol \ldots used in text mode to make an ellipsis (\(\ldots\)).  This is also a valid symbol in math mode, and can be very useful for lists (e.g. \(1,2,3,\ldots,100\)).  In addition to this, \cdots is also a command in math mode.  This will centre the ellipsis vertically with the text, useful when describing a series of additions or multiplications (e.g. \(1+2+3+\cdots+100\) or \(1\times2\times\cdots\times10\)).

This is just a small collection of symbols.  If there is a symbol you wish to use, there is likely a command for it.  The Comprehensive LaTeX Symbol List contains over 5900 LaTeX symbols! Searching for a symbol can also be done with Detexify, a web application which will give a list of possible commands based on a drawn image. If neither option is effective at finding what you are looking for, searching the web for information is the next best step.

Package Symbols

Be aware that many of the symbols you will find using the methods above will require you to include a package (which should be listed with the symbol itself).  The symbols we introduce in this section (and others you will encounter in future lessons) may require either the amssymb package or the amsmath package.  You may want to make these standard packages you include in all documents, since the symbols in these packages are used often.

Non-italicized Text in Math Mode

As we have discovered, text in math mode is automatically italicized.  It is assumed that any letters included are intended to represent variables.  But, there are cases in which we want to include non-italicized text.

One instance of this would be function names, such as the trigonometric functions sin, cos, etc.  For many commonly used functions, LaTeX has self named commands which will print the function name in non-italicized text.  For example,

$$ \lim_{x \rightarrow \infty} \frac{\sin x}{x} = \cos (90^{\circ}) $$

displays as

You may want to experiment a little to see if there are any other function names that can be used in this way.  In particular, you’ll notice that \mod is not a function, but try experimenting with \bmod and \pmod{n} to see what you get.

There are bound to be cases where function names do not have a command, or when one desires to put several words of plain text into an equation.  In these cases, we can use the \textrm{} command.  This command will format any text according to the default serif font in the document’s text mode (see the next lesson for more on fonts).  It also treats whitespace the same as it would in text mode.  Let’s look at an example:

$$ \textrm{Number of tickets sold} \times \textrm{Price of one ticket} = \textrm{Total Revenue} $$

displays as

\[\textrm{Number of tickets sold} \times \textrm{Price of one ticket} = \textrm{Total Revenue}\]

\left and \right Parentheses in Math Mode

In math mode or displaymode, parentheses ( ) are always typeset the same.  This can be a problem for math symbols taller than one line of text.  For example,

$$ (\frac{a}{b})^2 = \frac{a^2}{b^2} $$

displays as

Ideally, we would want the height of the parentheses to match the height of the math it contains.  This can be done by placing \left before the open parenthesis ( and \right before the closed parenthesis ), as demonstrated below:

$$ \left( \frac{a}{b} \right)^2 = \frac{a^2}{b^2}

displays as

This works with symbols other than parentheses too, including square brackets [ ], braces \{ \} and vertical lines | | to name a few.

Note that \left and \right must always be used together in order to tell LaTeX the selection of math for which it needs to match the height.  If for some reason you only need one large symbol, place a period after \left. or \right. to make it a placeholder.

There is another command called \middle that is optional, and this can be used in-between any \left and \right commands.  Here is an example where a middle command might make sense:

The cross ratio of four numbers is defined to be
$ (a,b;c,d) = \left. \frac{a-c}{c-b} \middle/ \frac{a-d}{d-b} \right. $

displays as

You may find special functions which will take care of the \left and \right for you. \binom{n}{i} (which uses the amsmath package) is such a command; it will adjust the parentheses based on whether it is inline or in display mode. The name comes from “binomial coefficients.”

There are other spaces you can use! As a rule of thumb, we don’t really care too much about fiddling around with this because it can be very time-consuming, and getting the spacing right is as much as an art as a science. But in the example above it looks too weird if you leave it out completely! Here’s a list of types of spaces in increasing size (consider it as optional material).

• \! (backslash-exclamation point, negative thin math space)
• \, (backslash-comma, thin math space)
• \: (backslash-colon, medium math space)
• \; (backslash-semicolon, thick math space)
• \  (backslash-space, a space character)
• \quad (“em” space of width equal to the current font size height)
• \qquad (two em spaces)
• \hspace{«length»} if you want to force a specific length